A curve is basically a continuous line that is not straight. It can be smooth, like splines, or made up of connected straight segments, like polylines. Applications are widely and can come in subtle forms, such as the creation of fonts that we use to write in our technological devices. In this project, I start implementing the parametric formulas of Cubic Bézier curves and Cubic B-splines to create curves and piecewise curves in the 2D space to poosteriorly used in the base contruction of surfaces of revolutions and generalized cylinders.
Bézier curves applied to font design by Ben Barnhart.

Note
The framework of this project is available in the Computer Graphics course from MIT OpenCourseWare. Check the references part for links!
Project objetive
Create a tool that implements parametric cubic curves (B-splines and Bézier) to generate swept surfaces to model interesting shapes.
Note
Before diving into the details of the project, I feel it is necessary to introduce some relevant concepts that may be new to the reader. This conceptual foundation will make the project easier to understand, I hope so. Feel free to skip ahead to the sections that interest you. If you are curious about the mathematics behind these parametric cubic curves, I invite you to visit my blog and read the post titled Understanding the Math Behind Parametric Curves.
Curves in Computer Graphics
The topic of curves and their applications is vast and immensely diverse. It’s hard to fully grasp the breadth of their uses. Depending on your needs and goals, there is a wide range of curves available for study and implementation.
In the field of computer graphics, the objectives behind the application of curves are to create smooth curves, provide high user control, and minimize computational expense (reducing time consumption). To achieve these goals, developers and technical teams typically use parametric cubic curves under de hood, which offer a good balance of these requirements. The most common applications of these cubic curves are: Cubic Bézier and Cubic Splines.
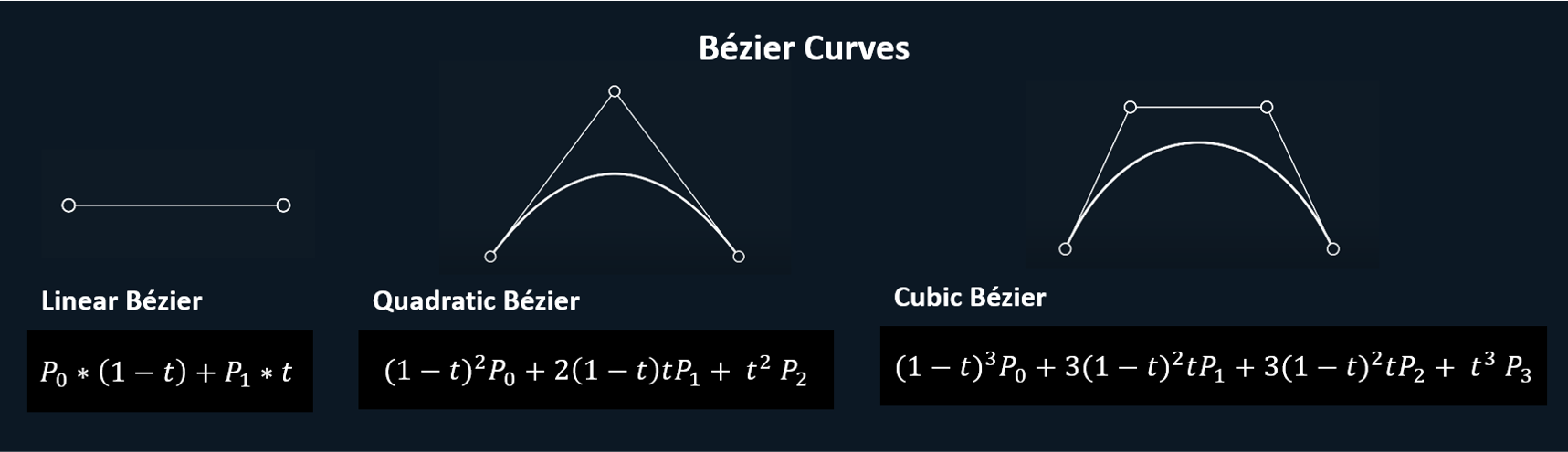
Cubic Bézier curve
A cubic Bézier curve is a type of parametric curve defined by four points: two endpoints and two control points. The curve starts at the first endpoint, moves towards the first control point, bends towards the second control point, and ends at the second endpoint. The positions and distances of the control points influence the shape and curvature of the Bézier curve. The curve is generated by interpolation.
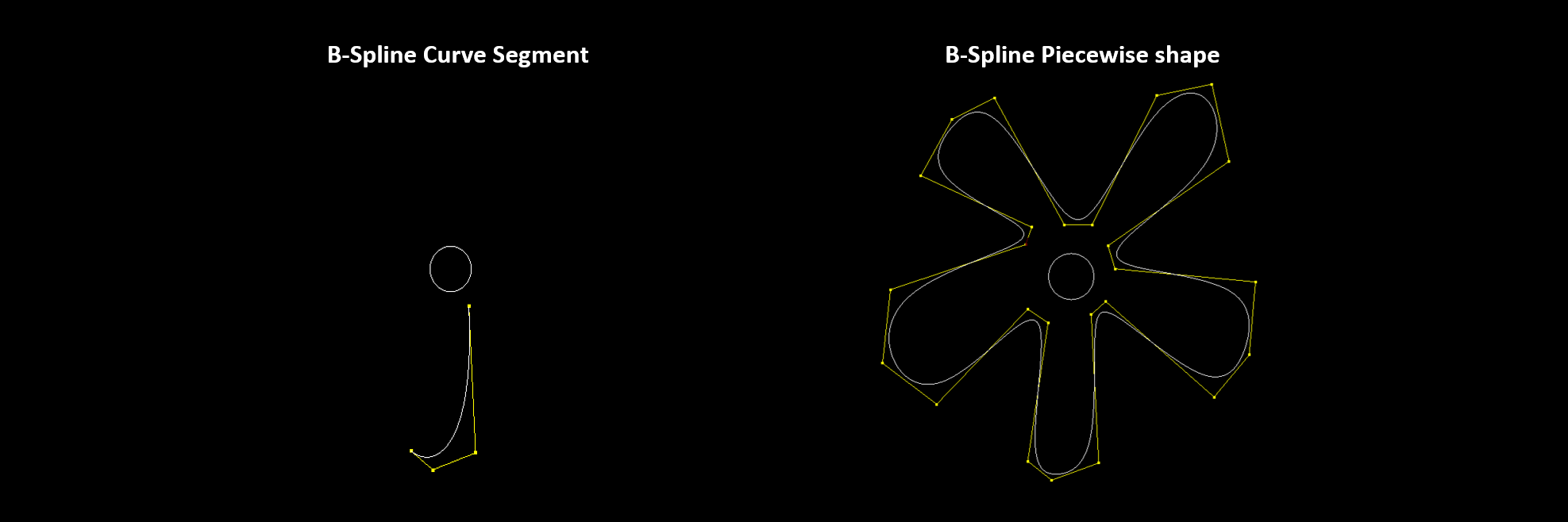
B-Spline
B-Splines are a type of spline with polynomial segments of degree 3. They are defined by control points that shape the curve and a knot vector, which is a sequence of values determining how the control points affect the curve. The curve is smooth and continuous because the mathematical functions used ensure that it transitions smoothly between segments. Unlike Bézier curves, B-Splines are not created by interpolation, which means they do not necessarily pass through the control points.
Piecewise Curves Construction
This is a method to connect simple curves, such as Bézier or B-splines, to create more complex shapes. Each curve acts as a segment defined by its own equation, and together, these segments form the entire shape.
With B-splines, to create smoothness, you connect the first four points, define the curve segment, and then move one point forward, ignoring the first point. For example, points 1-2-3-4 define the first segment, the next segment is defined by points 2-3-4-5, and then points 3-4-5-6 define the following segment, and so on.
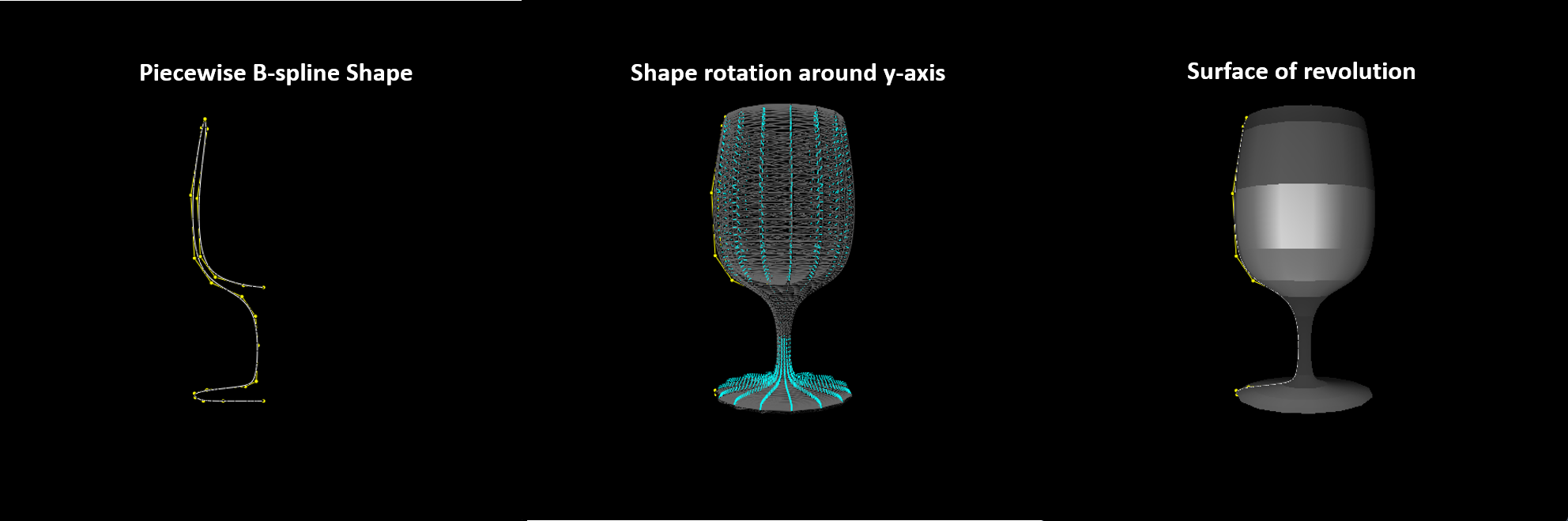
Surfaces of revolution
Surfaces of revolution are formed when a curve or piecewise curves is rotated a full 360 degrees (or 2π radians) around an axis as the x-axis, y-axis or z-axis. The resulting surface encloses a volume corresponding to the area swept out by this rotation.
The image depicts a wineglass shape defined by around 10 B-spline curves. To create a smooth surface in OpenGL, the shape is rotated by 24 degrees, generating an additional 15 piecewise curves. Each curve seamlessly blends points with the next, facilitating OpenGL’s surface creation process.
Generalized cylinders
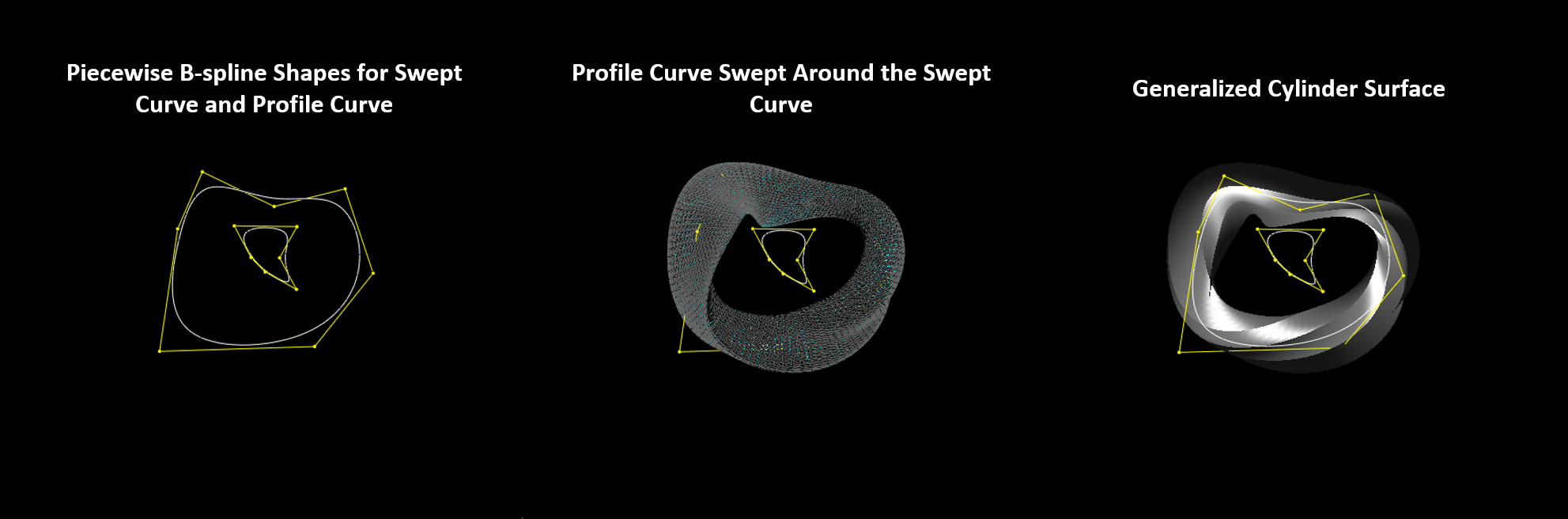
Generalized cylinders are formed by two curves: a piecewise curve known as the sweep curve, which represents the path, and another curve called the profile curve, defining the cylinder’s cross-sectional shape.
The shape depicted in the image is formed by sweeping a profile curve along a path defined by another curve. Initially, the profile undergoes transformations like rotation and translation to align it perpendicularly to the path defined by the swept curve. Similar to creating a revolution surface, multiple profile curves are generated along the swept path, blending points between consecutive profiles. These profiles are then used to generate a mesh or surface, resulting in the final 3D shape.
Project structure
-
Camera.h: Contains settings related to the project’s camera, such as dimensions, perspective, viewport, and instructions for camera manipulation including rotation, zoom, and translation to different perspectives.
-
Curve.h: Defines a struct CurvePoint that stores vertex, tangent, normal, and binormal information for each point on the curve. Provides functions evalBezier and evalBspline for evaluating Bézier and Bspline curves respectively, using a vector of control points and a parameter for step or point creation. Also includes evalCircle and a function drawCurve.
-
Extra.h: Contains inline functions to assist with the drawing process, such as glVertex, glNormal, glLoadMatrix, and glMultMatrix.
-
Paser.h:: defines functions and structures for parsing a custom file format (“SWP”) used to describe spline curves and swept surfaces. The format allows specifying various types of curves (Bézier/Bspline) and surfaces (circles, surfaces of revolution, generalized cylinders) with specific parameters like name, steps, and control points.
-
Surf.h: Defines structures and functions for working with surfaces, including operations like drawing surfaces with or without shading, drawing normals, creating surfaces of revolution (makeSurfRev), creating generalized cylinders (makeGenCyl), and outputting surfaces in OBJ file format (outputObjFile).
-
Tuple.h: This tuple class template provides functionality for creating and manipulating tuples of a fixed size (SIZE) with elements of type TYPE. It includes constructors for variadic initialization, array initialization, copy constructor, assignment operators, and indexing operators.
Technology
- Programing lenguage : C++17
- Graphic API: OpenGL
- Utility Toolkit: freeglut.
Creation process
When enhancing the MIT framework, the focus is on integratinng Bézier and B-Spline curves. This involves precise calculations using their respective cubic formulas to determine the position of each point. Derivatives play a crucial role in computing additional vectors: the tangent, normal, and binormal. Specifically, the tangent vector is derived from the first derivative of the Bézier curve, while the normal is derived from the second derivative. The binormal is then obtained through the cross multiplication of the tangent and normal vectors.
Following this implementation, the next steps include adding functionality for wisepice curves and refining the logic for generalizing cylinders.
Lessons Learned
-
Matrix Transformation: In matrix transformations, the order of operations is crucial for accuracy. I recommend experimenting with the multiplication order of matrices to understand its impact on the final transformation result.
-
Vector Libraries: A reliable vector library is essential for efficiently performing complex calculations. Ensure your library supports essential operations such as matrix and vector multiplication, cross products, dot products, normal calculations, vector normalization, and more.
-
Mesh Generation in OpenGL: Understanding how to render triangles as meshes is fundamental for graphical applications. Ensure that the order of indices of the points defining each triangle surface is acceptable to OpenGL. If the indices are not in the correct order, you may need to use techniques like the z-buffer to correctly generate triangle meshes.
-
Normal Directions: Properly defining the direction of normals is crucial for achieving realistic and visually appealing renders. During the rendering process, light calculations depend on the angle between the surface normal and the incident light direction. If your normals point in the wrong direction, it becomes impossible to accurately calculate lighting values for your mesh, resulting in rendering issues.
Note
Everything we create in computer graphics is an approximation. The tools I’ve developed and I will are no exception. From the underlying technology to the implementation by artists, every participant in the chain strives to approximate reality as accurately as possible within their control.
References
Ref[1] = https://www.linearity.io/blog/bezier-curves/
Ref[2] = https://ocw.mit.edu/courses/6-837-computer-graphics-fall-2012/pages/assignments/
Ref[3] = https://mmrndev.medium.com/understanding-b%C3%A9zier-curves-f6eaa0fa6c7d
Ref[4] = https://www.geeksforgeeks.org/b-spline-curve-in-computer-graphics/