Understanding the Mathematics of Major Parametric Cubic Curves

Parametric polynomial curves are defined by polynomial functions of a parameter, such as time, steps, or angle. These curves are valued for their smoothness and ease of manipulation and control. Although these curves can be of any polynomial degree, parametric cubic curves are often preferred. Lower-degree curves offer too little flexibility in shaping the curve, while higher-degree curves can introduce unwanted wiggles, result in a loss of local control, and require more computation.

In this discussion, we explore key parametric cubic curves such as Cubic Bézier, Hermite Splines, and B-Splines. Coming soon, I plan to post a detailed discussion on Catmull-Rom curves.

#Recommedation

I highly recommend following and supporting the work of Freya Holmér. Her explanations of splines and Bezier curves are exceptional and insightful. You can find her engaging content on these topics at Freya Holmér’s YouTube Channel.

Mathematically expressions

A curve, which is a geometric object, can be expressed in mathematical terms using explicit functions, or implicit and parametric equations.

Note

Equations and functions are not the same; there exists a subtle distinction based on dependency. In functions, variables act independently to determine the values of dependent variables. In contrast, equations typically express relationships between variables without explicitly defining independence or dependence.

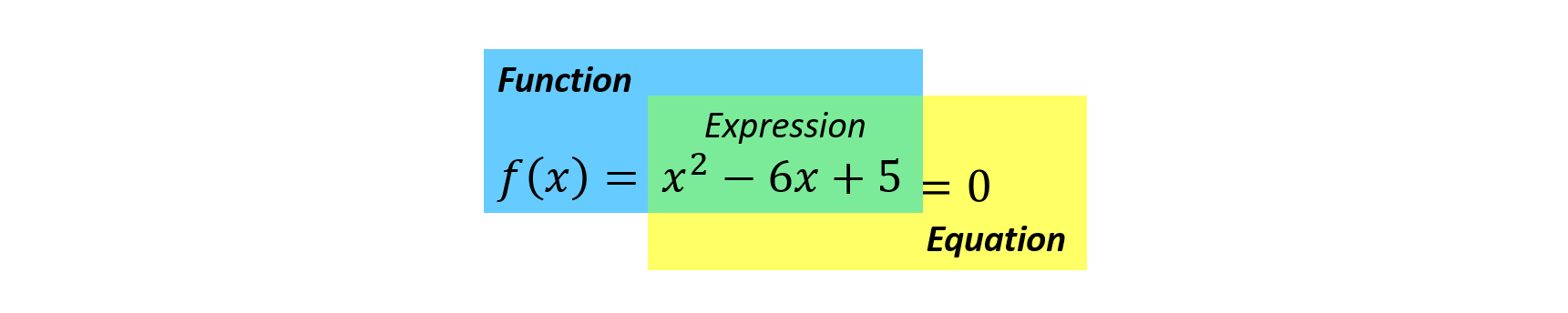
function-equation-diff

Explicit functions: Explicitly functions describe geometry by directly expressing one variable in terms of another. These functions are straightforward in defining relationships such as $ 𝑦 =𝑓(𝑥) $ where each point’s coordinates determine its position relative to the function’s parameters.

Note

Geometry objects often described explicitly can alternatively be expressed implicitly, but resolving them is more challenging. So, why would one choose implicit forms? Because sometimes we encounter complex functions that cannot be solved explicitly, and what we have to do is rewrite the original as an equation $f(x,y)=0 $ and attempt to solve it.

Implicit equations: Implicit equations describe geometry that is compose by points that satisfy the equation. The geometry objects that usually be describe it in an implict form are curves, but not are the only one, more complex surfaces can be describe it also.

The next table inclose some examples of curves defined in a implicit way in a 2D and 3D space

Curves (2D)	Equation	Surfaces (3D)	Equation
Circles	$ (x - h)^2 + (y - k)^2 - r^2 = 0 $	Spheres	$ (x - h)^2 + (y - k)^2 + (z - l)^2 - r^2 = 0 $
Ellipses	$ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} - 1 = 0 $	Ellipsoids	$ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} + \frac{(z - l)^2}{c^2} - 1 = 0 $
Hyperbolas	$ \frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} - 1 = 0 $	Hyperboloids	$ \frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} + \frac{(z - l)^2}{c^2} - 1 = 0 $

Note

The curve itself is a one-dimensional object that can exist in different dimensions.

Parametric equations: Pametric equations describe geometry where each coordinate of a point in space is expressed as a function of one or more independent parameters. These parameters often represent time, angles, or other variables that dictate how the coordinates evolve. Parametric equations provide a flexible way to model complex shapes and motions, allowing for detailed control over the geometry’s characteristics and behavior.

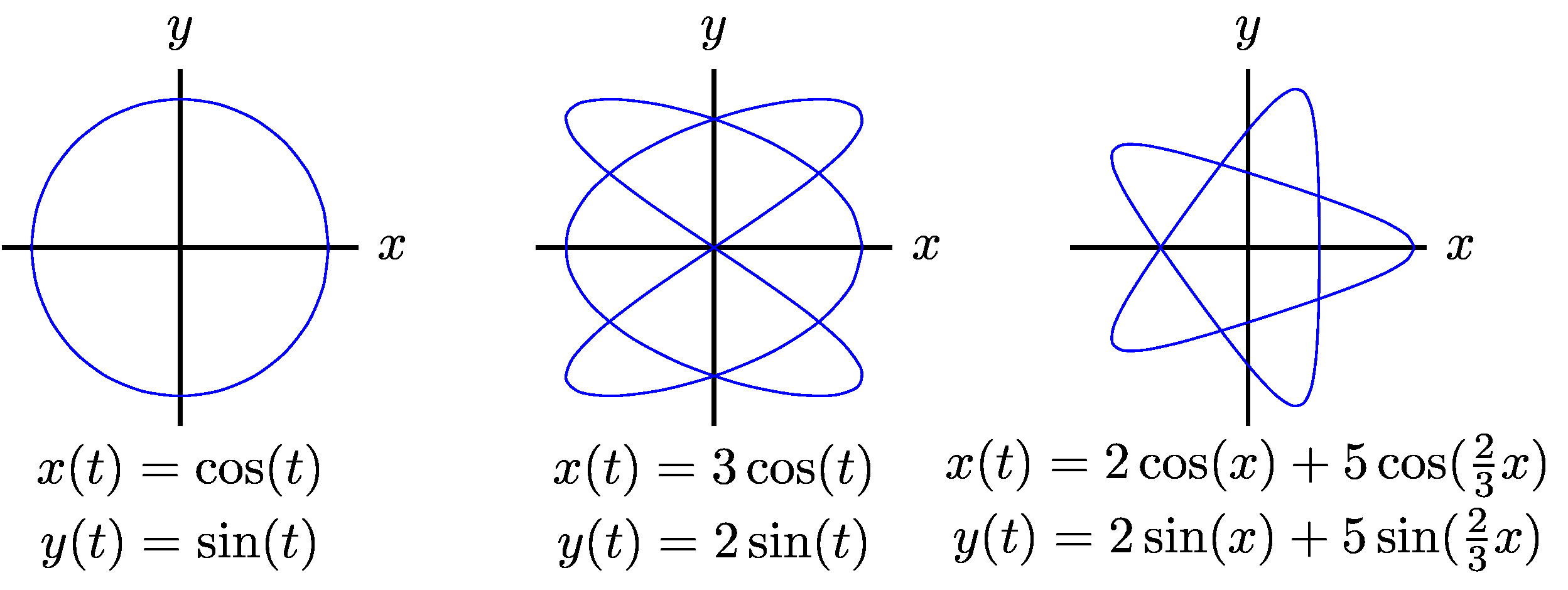
parametric-equation

Change of Basis

A parametric cubic curve is defined by a third-degree polynomial, needing four control points to describe its shape. The position of these points determines the curve’s form. If you use a curve generator such as Bezier curves, B-splines, or others with the same control points, you might not obtain the same curve because each method uses a different basis. However, by correctly adjusting the basis of the control points, you can recreate the same curve. Therefore, accurately identifying the method used to generate a curve becomes challenging without additional contextual information.

In algebra, a basis is a concept that can be abstract, but it’s useful to think of a basis as a reference frame or a language. Just like languages have different words for the same objects, different bases have different ways of defining points. To get equivalent descriptions, you need to “translate” the points from one basis to another. This change of basis is achieved by multiplying the vectors (which represent the positions of the points) by the matrix that performs the basis change.

Exercise

For example, imagine you have four control points defined as (x,y,z,0) for a B-spline curve, and you want to visualize the same curve in the Bézier basis. Here’s what you need to do:

Organize the points into a 4x4 matrix and named as orginalBasisPoints.
Use the B-spline basis matrix, which is: $$ Basis_{BSpline} = (1/6) \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} $$
Use the Bézier basis matrix: $$ Basis_{Bézier} = \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} $$
Apply the inverse of the Bézier basis matrix to get: $$ Basis^-1_{Bézier} = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1/3 & 1 \\ 0 & 1/3 & 2/3 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix} $$
Multiply the matrices in sequence as follows: $$ NewPoints = Points * Basis_{BSpline} * Basis^-1_{Bézier} $$

Note

Matrix multiplication occurs in the opposite order (backward). If you want to organize the opperations above in a matrix order the process can be something like this:

$$ NewPoints = Basis^-1_{Bézier} * Basis_{BSpline} * Points $$

but its just a mathematical convention. Don’t confuse yourself.

Continuity

When two curves are joined, we typically want some degree of continuity across the knots (unions). This continuity can be geometric and parametric.

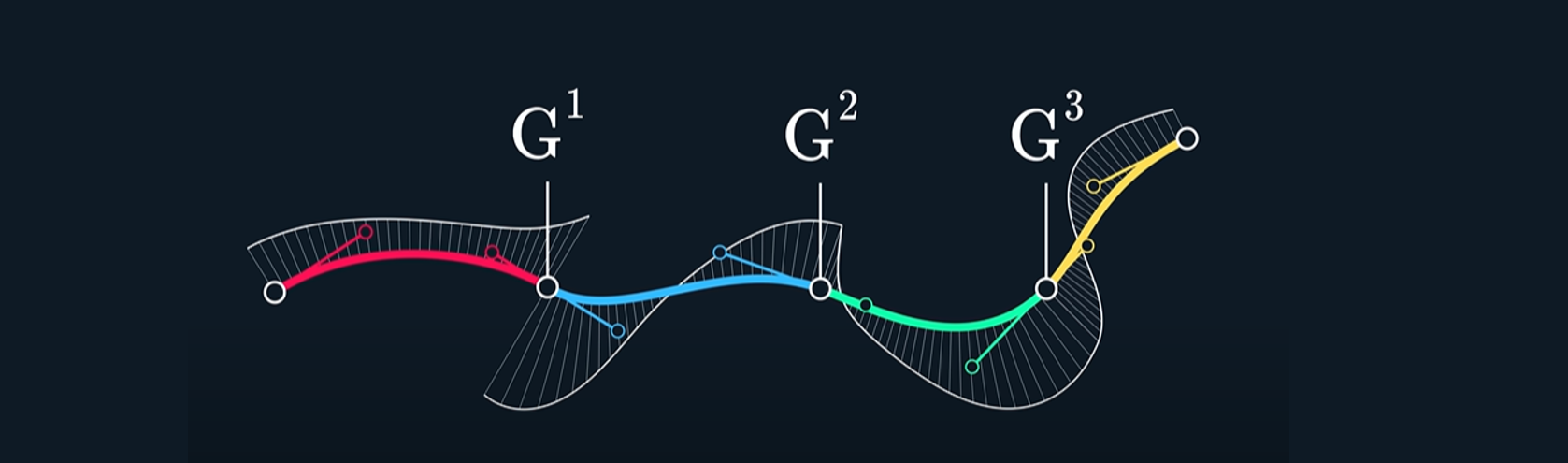
Geometric Continuity: Ensures that the curves meet smoothly. There are different level of geometric continuity:

G0 Continuity: The curves are connected; their endpoints meet.
G1 Continuity: The curves have the same (tangent) direction at the join point, ensuring no sharp corners.
G2 Continuity: The curves have the same (curvature) at the join point, providing an even smoother transition.
G3 Continuity: The curves have the same rate of change of curvature (torsion) at the join point, resulting in the highest level of smoothness.

G-continuity

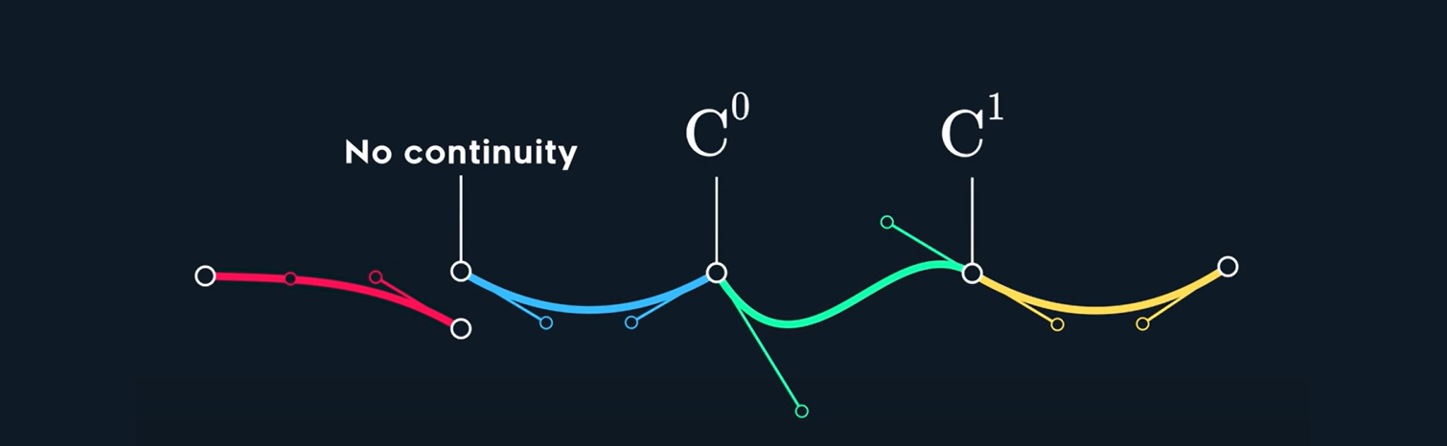
Parametric Continuity: Ensures that the parameter values of the curves match at the joining point, maintaining a smooth progression of the parameter along the curve. This involves matching higher derivatives (like velocity and acceleration) to ensure smooth transitions in the shape and speed of the curve.

C0 Continuity: The curves are connected; their endpoints meet.
C1 Continuity: The first derivatives (velocity) of the curves are equal at the join point.
C2 Continuity: The second derivatives (acceleration) of the curves are equal at the join point.
C3 Continuity: The third derivatives (jolt) of the curves are equal at the join point, ensuring the highest level of smoothness in the curve transition.

P-continuity

Piecewise Curves Construction

Piecewise curve construction is a method of creating complex shapes by connecting multiple simpler curve segments, ensuring smooth transitions between them. Here curves have at least C0 and G0 continuity.

Cubic Bézier

A cubic Bézier curve is one that uses four control points to define its shape. The first and last points are the endpoints of the curve, while the two middle points determine the curvature. By adjusting these control points, you can change the shape of the curve. Also the curve pass throught the origin and end point.

Cubic Bézier Parametric form

$$ P(t) = (1 - t)^3 P_{1} + 3t(1-t)^2 P_{2} + 3t^2(1-t) P_{3} + t^3 P_{4} $$

where:

$ t $ is a value between 0 and 1, calculated as follows: $ t = 1 - \frac{\text{nstep}}{\text{totalsteps}} $.
$ \text{nstep} $ is the current step.
$ \text{totalsteps} $ is the total number of steps for interpolation.
$ P(t) $ is the position on the curve at parameter $ t $.
$ P_1 $, $ P_2 $, $ P_3 $, and $ P_4 $ are the control points.

Cubic Bézier Matrix form

$$ P(t) = (t^3, t^2, t, 1) \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{pmatrix} P_{1} \\ P_{2} \\ P_{3} \\ P_{4} \end{pmatrix} $$

Three ways to calculate Bézier curves by Freya Holmér cubic-bezier

Note

In the picture above lerp is a function and means linear interpolation

B-spline

A B-spline (Basis spline) is a piecewise-defined curve that is represented by a set of control points. Unlike Bézier curves, B-splines do not necessarily pass through their control points. Instead, the control points influence the shape of the curve in a more global manner. B-splines offer great flexibility and local control, meaning that modifying one control point only affects a portion of the curve, rather than the entire curve. This makes B-splines particularly useful for complex shapes and smooth curve approximations.

B-spline Parametric form

$$ P(t) = (-1/6t^3 + 1/2t^2 - 1/2t + 1/6) P_{1} + (1/2t^3 - t^2 + 2/3) P_{2} + (-1/2t^3+ 1/2t^2 + 1/2t + 1/6) P_{3} + (1/6t^3)P_{4} $$

where:

$ t $ is a value between 0 and 1, calculated as follows: $ t = 1 - \frac{\text{nstep}}{\text{totalsteps}} $.
$ \text{nstep} $ is the current step.
$ \text{totalsteps} $ is the total number of steps for interpolation.
$ P(t) $ is the position on the curve at parameter $ t $.
$ P_1 $, $ P_2 $, $ P_3 $, and $ P_4 $ are the control points.

B-spline Matrix form

$$ P(t) = (t^3, t^2, t, 1) (1/6) \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{pmatrix} P_{1} \\ P_{2} \\ P_{3} \\ P_{4} \end{pmatrix} $$

Hermite Cubic Spline

A Hermite cubic spline is a type of spline where the curve is defined by its endpoints and the tangents (derivatives) at those endpoints. Specifically, each segment of the spline is determined by four values: the positions and tangents at the two endpoints. By adjusting these points and tangents, the shape of the curve can be altered. Hermite cubic splines are particularly useful for interpolating between points with specified slopes, ensuring smooth transitions between curve segments.

Hermite Parametric form

$$ P(t) = (2t^3 - 3t^2 + 1) P_{0} + (t^3 - 2t^2 + t) M_{0} + (-2t^3 + 3t^2) P_{1} + (t^3 - t^2) M_{1} $$

where:

$ t $ is a value between 0 and 1, calculated as follows: $ t = 1 - \frac{\text{nstep}}{\text{totalsteps}} $.
$ \text{nstep} $ is the current step.
$ \text{totalsteps} $ is the total number of steps for interpolation.
$ P(t) $ is the position on the curve at parameter $ t $.
$ P_0 $ and $ P_1 $ are the starting and ending points.
$ M_0 $ and $ M_1 $ are the starting and ending tangents.

Hermite Matrix form

$$ P(t) = (t^3, t^2, t, 1) \begin{bmatrix} 2 & -2 & 1 & 1 \\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{pmatrix} P_{0} \\ P_{1} \\ M_{0} \\ M_{1} \end{pmatrix} $$

How to choose the right parametric curve

Hermite Cubic Spline: Ideal for single segments where the parametric derivative is known, or when easy control over the tangents (derivatives) at the endpoints is needed.
Cubic Bézier: Suitable for single segments or patches where the user controls the points directly. These curves provide intuitive control over the curve’s shape through their control points.
B-Splines: Best for large, continuous curves and surfaces. They offer great flexibility and local control, making them well-suited for complex shapes and smooth curve approximations.

References

Ref.1 = https://www.linearity.io/blog/bezier-curves/

Ref.2 = https://wdv.com/Calculus/Lecture01.pdf

Ref.3 = https://mathbooks.unl.edu/Calculus/sec-3-7-parametric.html

Ref.4 = https://irc.cs.sdu.edu.cn/~lulin/course/3dmodeling/5_Parametric_Curves&Surfaces.pdf

Ref.5 = https://www.youtube.com/watch?v=aVwxzDHniEw&ab_channel=FreyaHolm%C3%A9r

Ref.6 = https://www.youtube.com/watch?v=jvPPXbo87ds&ab_channel=FreyaHolm%C3%A9r

Ref.7 = https://es.slideshare.net/slideshow/hermite-cubic-spline-curve-117230866/117230866

Ref.8 = https://www.geeksforgeeks.org/hermite-curve-in-computer-graphics/

Ref.9 = https://www.symbolab.com/

Curves (2D)	Equation	Surfaces (3D)	Equation
Circles	\( (x - h)^2 + (y - k)^2 - r^2 = 0 \)	Spheres	\( (x - h)^2 + (y - k)^2 + (z - l)^2 - r^2 = 0 \)
Ellipses	\( \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} - 1 = 0 \)	Ellipsoids	\( \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} + \frac{(z - l)^2}{c^2} - 1 = 0 \)
Hyperbolas	\( \frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} - 1 = 0 \)	Hyperboloids	\( \frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} + \frac{(z - l)^2}{c^2} - 1 = 0 \)

#Recommedation#

Mathematically expressions#

Note#

Note#

Note#

Change of Basis#

Exercise#

Note#

Continuity#

Piecewise Curves Construction#

Cubic Bézier#

Note#

B-spline#

Hermite Cubic Spline#

How to choose the right parametric curve#

References#

#Recommedation

Mathematically expressions

Note

Note

Note

Change of Basis

Exercise

Note

Continuity

Piecewise Curves Construction

Cubic Bézier

Note

B-spline

Hermite Cubic Spline

How to choose the right parametric curve

References